Las sucesiones infinitas y la moral pública

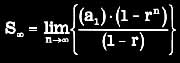
(Aviso: este artículo contiene unos extraños objetos arcanos llamados “números” que pueden dar dolor de cabeza a los que los miren fijamente)

Una de las disciplinas matemáticas más fascinantes que se estudian ya en el colegio o instituto son las sucesiones infinitas. Estas sucesiones son conjuntos de números sucesivos con una particularidad significativa: el número de elementos de las mismas no se acaba nunca.

1 2 3 4 5 6…

0,1 0,01 0,001 0,0001 0,00001…

0 0,5 0,75 0,875 0,9375…

Lo fascinante de estas sucesiones estriba en que, a pesar de tener términos infinitos, podemos realizar operaciones con ellas. Si bien es cierto que, como seres limitados que somos, el infinito nos supera, nos desborda, nuestro intelecto es capaz de remontarse en algunos casos a ese infinito e, incluso, de realizar operaciones con estas sucesiones de elementos infinitos. Podemos, por ejemplo, sumar sus términos (las “series infinitas”) y, en muchos casos, el resultado de esta suma de términos infinitos converge, es decir, tiene un resultado finito, que podemos comprender.

Estas series, que resultan fascinantes en el estudio de las matemáticas, pueden utilizarse también en otras disciplinas, ya que, a fin de cuentas, las matemáticas son herramientas que nos ayudan a comprender mejor la realidad. Al igual que pueden utilizarse en Física, Biología y otras ciencias naturales, en mi opinión también pueden utilizarse con cierto provecho en disciplinas humanísticas como la filosofía, antropología, metafísica y teología (usos que podríamos estudiar en otros posts si los lectores están interesados). En este artículo, sin embargo, me voy a fijar únicamente en la luz que pueden arrojar sobre el tema de la moral pública.

Hoy en día, en buena parte debido a nuestro estilo de democracia, la moral pública es, esencialmente, una moral de consenso. Diversos políticos, filósofos e, incluso, teólogos, ponderan una ética de mínimos que consiste, a grandes rasgos, en aquello en lo que la mayoría estamos de acuerdo en el ámbito moral.

Vamos a intentar dar un poco de luz sobre esta moral de consenso utilizando las sucesiones infinitas. El tercer ejemplo de sucesión que incluí como ejemplo refleja, aunque no lo parezca, cómo funciona un cierto tipo de consenso moral.

Digamos que el punto 0 y el punto 1 representan dos posiciones enfrentadas sobre un tema moral cualquiera. Si la posición 0 y posición 1 representan ambos extremos de la cuestión, el consenso podría representarse como aproximadamente el punto 0,5, equidistante entre ambas. Por ejemplo, en un país que nunca se ha planteado el tema de legislar sobre el aborto, la postura 0 podría ser la prohibición total y la postura 1 el aborto libre y gratuito sin limitaciones. Un primer consenso, en el punto medio 0,5, sería, probablemente, la aceptación del aborto en casos de peligro para la madre o violación.

0 ——————– 0,5 —————— 1
Prohibición ———-Consenso———-Libertad

El tema podría, en principio, quedarse ahí, en el punto medio de consenso o punto 0,5. Sin embargo, como nuestra sociedad lo que valora por encima de todo es el alcanzar un consenso, sucede algo muy curioso: si una de las posturas acepta el consenso, pero la otra permanece firme en su posición inicial, vuelve a faltar el consenso. De nuevo comienza el proceso de lograr un acuerdo que satisfaga a todos, pero ahora las posiciones extremas son 0,5 (la del grupo que aceptó el primer consenso) y 1 (la del grupo que ha permanecido firme en su posición inicial). El consenso ahora se alcanza en el punto 0,75. En el ejemplo del aborto, el consenso entre los que han aceptado los supuestos de despenalización (punto 0,5) y los que han seguido exigiendo el aborto libre (punto 1) se alcanza en la aceptación de un nuevo supuesto “amplio” relativo a la salud física y síquica de la madre.

0 ———————— 0,5 ———–0,75————– 1
————————2 sup————-3er sup——Libertad

Si ahora, de nuevo, sucede lo mismo, unos aceptan ese nuevo consenso pero otros siguen firmes en su postura inicial, el proceso actúa de nuevo y alcanza un tercer consenso en el punto 0,875.

Se puede ver que ésta es la serie que incluí al principio y, matemáticamente, es fácil demostrar que, si avanzamos lo suficiente, esta serie converge en el punto 1.

0 0,5 0,75 0,875 0,9375… 1

Es decir, esta sucesión de consensos entre una postura fija y otra que va cediendo termina por ser prácticamente idéntica a la postura fija. En nuestro ejemplo del aborto, termina indefectiblemente en el aborto libre y gratuito, sin limitaciones.

Este proceso no es algo puramente ideal, podríamos señalar muchos ejemplos reales que se han producido o que se están produciendo en España: el reconocimiento social de la homosexualidad, el aborto que ya en la práctica es libre, la aceptación de la eutanasia, las “conquistas” de los nacionalismos, etc.

¿Cuál es el único remedio para no ser desbordado por esta dinámica? Una distinción clara entre lo que Benedicto XVI ha llamado “principios innegociables” y elementos accesorios. Mantenerse firme en aquello que es innegociable hará que, a la larga, el principio del consenso actúe en nuestro favor. Si bien en lo accesorio y mudable se debe ser flexible para facilitar la convivencia, en los puntos innegociables hay que ser absolutamente firmes, sin transigir en lo más mínimo. Y si eso implica ser perseguidos… dichosos nosotros, porque también así persiguieron a nuestro Señor.